Reverse Time Holography method (RTH)
Summary
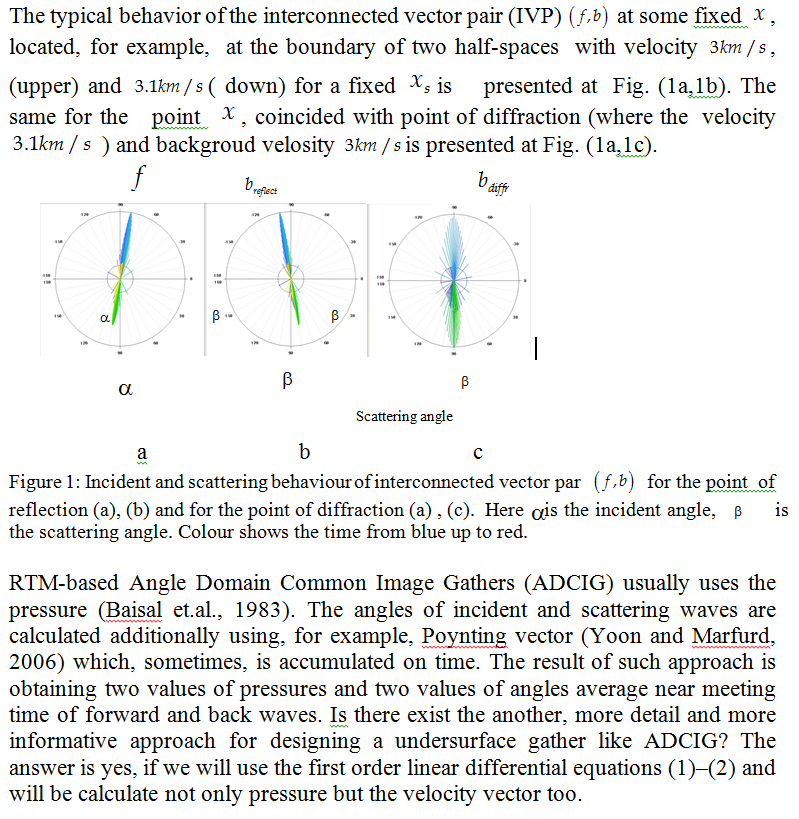
The process of scattering the acoustical wave on an obstacle at any moment of time may be considered as an interaction of two interconnected vectors: the particle velocity vector of the incident wave and generated by scattering the vector of the reflected or scattered wave. Mathematical method the inversion of the wave front in time based on the differential equations of the first order allows investigating such interaction more carefully. Proposed Vector Pair Reverse Time Migration method demands large storage memory and high computer performance but provides the new opportunities for studying the environment.
Introduction
The Reverse Time Migration (RTM) image processing (Baysal et.al.,1983; Whitmore, 1983; McMechan, 1983) is wide using for constrain the Common Image Gather (CIG) in Angle Domain (AD). The method RTM has the own internal artefacts because the method is based on the wave-equation. For overcoming such interference the image regularization is performed by filtration in an extended spaces ( including the ADCIG) of angle parameters (Yoon and Marfurd, 2006; Sava and Fomel, 2006; Zhang and McMechan, 2011). Despite the growing the performance of computer, there exist opinions, that using the RTM in full extended spaces is still very expansive (Vyas et.al., 2011, Guan et.al., 2013).
Nevertheless Erokhin et. al., 2017, suggested the new Reverse Time Holography method (RTH)) method, which really demands relatively large memory and high computer performance, but it seems that method provide the new opportunities for studying the environment. We propose the new conception the extraction and regularization, by the RTH method, of information for CIG, which allows us to create new subsurface images based on the new Imaging Conditions.
Method
Discussion
The distinctive feature of the proposed RTH method is incorporation the velocity vector in procedure of extraction the information for designing extended CIG. Proposed Vector Domain CIG contain essentially more information and more possibility regularization of image processing. The method introduces higher requirements to the hardware, but it makes it possible to calculate many interesting attributes simultaneously. Especially this is concern with the phase attributes. The new suite of attributes, calculated simultaneously, gives us the good perspective to interpret obtained information together, using a powerful statistical tool.
References
Baysal, E., D. D. Kosloff, and J. W. C. Sherwood, 1983, Reverse time migration: Geophysics, 48, 1514–1524, doi: 10.1190/1.1441434.
Erokhin G., Pestov L.,Danilin A., Kozlov M., and Ponomarenko D., 2017, Interconnected vector pairs image conditions: New possibilities for visualization of acoustical media, 2017, SEG Technical Program Expanded Abstracts 2017: 4624-4629., https://doi.org/10.1190/segam2017-17587902.1
Guan H., Williamson P., Denel B., Audebert F., and B. Duquet, 2013, Angle-domain common-image gathers extracted from pre-stack RTM images. SEG Technical Program Expanded Abstracts 2013: pp. 3767-3772. https://doi.org/10.1190/segam2013-1149.1
Koren Z., Ravve I, 2011, Full-azimuth subsurface angle domain wavefield decomposition and imaging Part 1: Directional and reflection image gathers; Geophysics, 76, S1-S13.
McMechan, G. A., 1983, Migration by extrapolation of time-dependent boundary values: Geophysical Prospecting, 31, 413–420, doi: 10.1111/ j.1365-2478.1983.tb01060.x.
Moser T.J. and C.B.Howard, 2008, Diffraction imaging in depth. Geophysical Prospecting, 56, 627–641 doi:10.1111/j.1365-2478.2007.00718.x
Ren Li, Liu Guofeng, Meng Xiaohong, Wang Jun, and Zhang Sheng ,2013, Suppressing Artifacts in 2D RTM Using the Poynting Vector. Near Surface Geophysics Asia Pacific Conference, Beijing, China 17-19 July 2013: pp. 484-487. https://doi.org/10.1190/nsgapc2013-112
Sava, Paul, and Sergey Fomel, 2006, Time-shift imaging condition in seismic migration: Geophysics, 71, no. 6, S209–S217.
Stolk, C. C., M. V. de Hoop, and T. Op’t Root, 2009, Linearized inverse scattering based on seismic reverse-time migration: Proceedings of the Project Review, Geo-Mathematical Imaging Group (Purdue University, West Lafayette IN), 91–108.
Vyas, M., D. Nichols, and E. Mobley, 2011, Efficient RTM angle gathers using source directions: 81st Annual International Meeting, SEG, Expanded Abstracts, 3104–3108.
Whitmore, N. D., 1983, Iterative depth migration by backward time propagation:53th Annual International Meeting, SEG, Extended Abstracts,382–385.
Whitmore N. D., and Sean Crawley, 2012, Applications of RTM inverse scattering imaging conditions: 82nd Annual International Meeting, SEG, Expanded Abstracts, doi: http://dx.doi.org/10.1190/segam2012-0779.1
Xie, X., and R. S. Wu, 2002, Extracting angle domain information from migrated wavefields: 72nd Annual International Meeting, SEG, Expanded Abstracts, 1360–1363.
Yan, R., and Xie, X.-B., 2009, A new angle-domain condition for prestack reverse-time migration: 79nd Annual International Meeting, SEG, Expanded Abstracts, 2784-2788
Yoon, K., and K. J. Marfurt, 2006, Reverse-time migration using the Poynting vector: Exploration Geophysics, 37, 102–107.
Zhang, Q., and G. A. McMechan, 2011, Direct vector-field method to obtain angle -domain common-image gathers from isotropic acoustic and elastic reverse-time migration: Geophysics, 76, no. 5, WB135–WB149, http://dx.doi.org/10.1190/geo2010-0314.